In this post I will try my best to explain my latest work, the Signed Dual Attention (SDA) mechanism, developed with Tristan Cazenave as part of my PhD and presented at the AI4TS workshop (AAAI 2026).
Table of Content
- How Rethinking Attention Led Me to SDA
- How Signed Dual Attention Works
2.1 Mathematical Formulation
2.2 Link with Two-Head Attention - Future Directions
How Rethinking Attention Led Me to SDA
This work began with a critical reflection on the Transformer architecture, inspired by my ongoing research on Graph Neural Networks. Attention can, in fact, be viewed as a fully connected graph. From this perspective, the attention matrix can be interpreted as a learned adjacency matrix.
Given my background in statistics and classical time series analysis, one of the most intuitive adjacency matrices that came to mind was the correlation matrix. Indeed, in terms of raw formulation, the similarity matrix corresponds to the correlation matrix when variables are centered and standardized. However, attention does not operate directly on a similarity matrix—it applies a softmax transformation to it.
This distinction leads to a crucial behavioral difference. A correlation matrix used as an adjacency matrix can represent signed relationships, allowing information to propagate with both positive and negative influences depending on the sign of the correlation. In contrast, a standard attention mechanism only permits positive influence. Why does attention still work despite this limitation? Because multi-head attention allows the model to learn multiple types of relationships.
However, this observation motivated me to explore the modeling of signed relationships within a single attention head. Why bother? Because relying on multiple heads to circumvent this theoretical limitation introduces inefficiencies. When two attention heads are used to learn opposite relationships, the corresponding keys and queries governing the same interaction must be learned twice. Furthermore, in conventional architectures, the feature dimension is divided by the number of heads, resulting in more parameters but less expressive capacity per head. It is from this inefficiency that the idea emerged—to design a mechanism that models both aspects of a relationship within a single attention head, using shared parameters.
How Signed Dual Attention Works
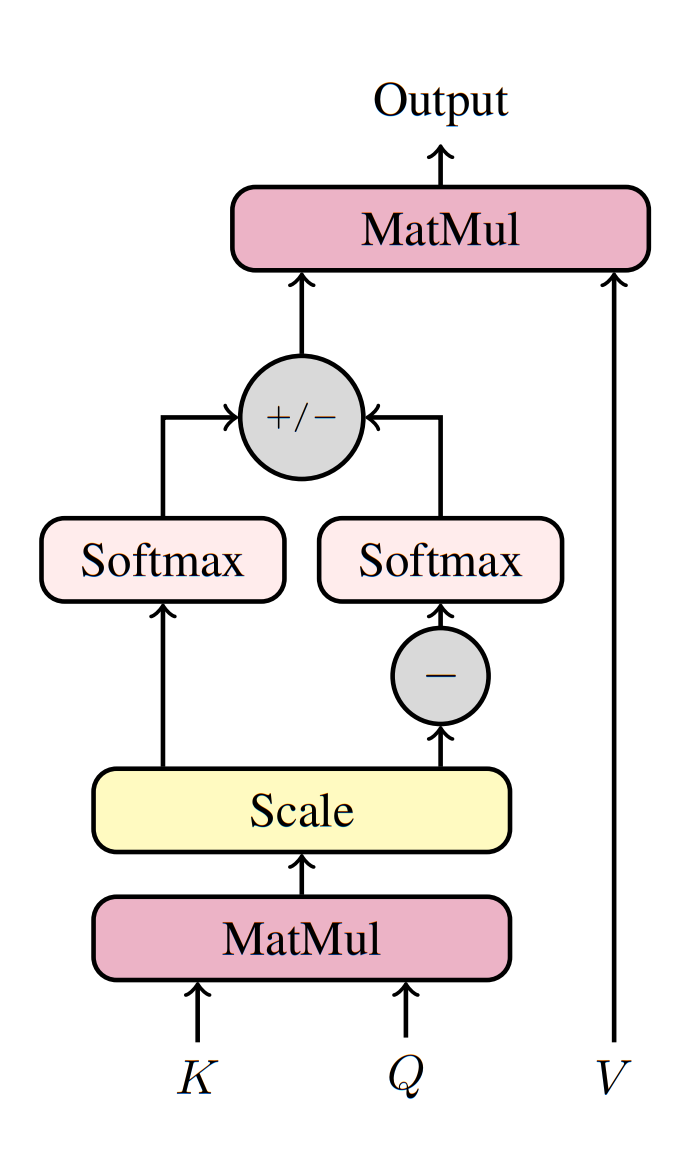
To model signed relationships, both positive and negative weights in the attention matrix are required. Previous works have addressed this by applying a $\tanh$ transformation to the similarity scores. However, I believe that the softmax function plays an essential role in ensuring stability and effective focus during attention computation.
The solution I adopted was therefore not to replace the softmax, but to extend it: by applying two softmax functions and constructing an odd function of the similarity matrix, the model can naturally encode both positive and negative affinities while retaining the desirable normalization properties of softmax-based attention.
Mathematical Formulation
SDA extends standard scaled dot-product attention by computing positive and negative attention matrices with shared keys and queries matrices:
\[\begin{align} A^+ &= \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right) \\ A^- &= \text{softmax}\left(-\frac{QK^\top}{\sqrt{d_k}}\right) \\ \end{align}\] \[\text{SDA}(Q,K,V) = (A^+ - A^-) V\]- $A^+$ propagates positive signals.
- $A^-$ propagates negative signals.
The subtraction ensures antagonistic relationships invert the message.
Link with Two-Head Attention
The Signed Dual Attention (SDA) block can be seen as a constrained form of a two-head self-attention mechanism. Imagine a standard two-head attention layer with parameters defined as
\[(W_1^K, W_1^Q, W_1^V) = (W^K, W^Q, W^V), \qquad (W_2^K, W_2^Q, W_2^V) = (-W^K,\, W^Q,\, -W^V).\]Let $H_1, H_2 \in \mathbb{R}^{T \times d}$ be the outputs of the two heads. In conventional multi-head attention, their concatenation $H_{\text{cat}} \in \mathbb{R}^{T \times 2d}$ is projected through an output matrix $W^O$ to obtain the final representation $H$ :
\[H = H_{\text{cat}} W^O.\]If we choose
\[W^O = \begin{bmatrix} I_d \\ I_d \end{bmatrix} \in \mathbb{R}^{2d \times d},\]the projection simply performs an additive fusion, leading to $H = H_1 + H_2$. Under this configuration, the output of the two-head mechanism aligns exactly with the SDA formulation.
This perspective highlights SDA as a compact and efficient alternative to multi-head attention—able to capture both supportive and antagonistic interactions while using half the parameter count and maintaining the computational footprint of a single-head layer.
Future Directions
Preliminary experiments suggest that SDA behaves differently across datasets depending on the underlying autocorrelation structure, particularly when both positive and negative dependencies coexist. This makes sense since by $W^O$ inforce both aspect of the relationship to have an equal influence, when it can depending of the data not be the case. I see potential in learning adaptive weighting between the positive and negative attention components $A^{+}$ and $A^{-}$ instead of assigning them equal importance. This enhancement could improve performance in settings where negative interactions are weak or primarily noisy.
